Polynomials¶

Polynomials are functions that have the form

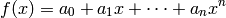
$f(x) = a_0 + a_1 x + \cdots + a_n x^n$

The coefficients 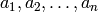$a_1,a_2,\ldots,a_n$ are often real numbers and 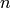$n$ which is a nonnegative integer, is the degree or order of the polynomial.

Representation¶

MATLAB uses a row vector to represent a polynomial, by the elements in the vector are the coefficients 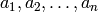$a_1,a_2,\ldots,a_n$ . The first element is the coefficient of the x with the highest power. The vector has to include all the coefficients, including the ones that are equal to 0. For example, the polynomial

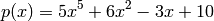
$p(x) = 5x^5+6x^2 - 3x + 10$

can be represented in MATLAB by typing:

>> p = [5 0 0 6 -3 10];

Value evaluation¶

The value of a polynomial at a point x can be calculated with the function polyval which has the form:

polyval(p,x)

where p is a vector with the coefficients of the polynomial and x is a value to be evaluated. x can also be a vector or a matrix. In these cases, the polynomial is calculated element by element. For example, with the polynomial p(x) given above, the value of p(0) can be computed by:

>> polyval(p,0)

ans =
    10

or if we want to evaluate p(x) at x = 0,1,2,3 at once, we can type:

>> polyval(p,[0 1 2 3])

ans =
          10          18         188        1270

The command polyval returns a vector with the corresonding values of the polynomial.

Hence, this make us an easier way to plot a polynomial function. Suppose we want to plot

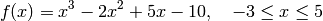
$f(x) = x^3-2x^2 + 5x -10, \quad -3 \leq x \leq 5$

We can use polyval for this purpose by typing:

>> p = [1 -2 5 -10];
>> x = linspace(-3,5,100);
>> px = polyval(p,x);
>> plot(x,px)

Roots of a polynomial¶

Roots of a polynomial

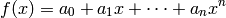
$f(x) = a_0 + a_1 x + \cdots + a_n x^n$

are the values of 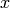$x$ for which 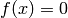$f(x) = 0$ . For example, the roots of 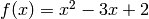$f(x) = x^2-3x+2$ are -1 and -2. There are n roots of a polynomial with degree n.

The command roots determines the roots of a polynomial. The usage of the function is:

r = roots(p)

where r is a column vector with the roots and p is a row vector with the coefficients of the polynomial. For example, the roots of

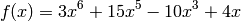
$f(x) = 3x^6+15x^5-10x^3 +4x$

can be found as follows:

>> p = [3 15 0 -10 0 4 0]

p =
     3    15     0   -10     0     4     0

>> roots(p)

ans =
        0
  -4.8613
  -0.6925 + 0.3093i
  -0.6925 - 0.3093i
   0.6232 + 0.2975i
   0.6232 - 0.2975i

Operations on polynomials¶

Addition¶

Two polynomials can be added or subtracted by adding the vectors of the coefficients. If the two polynomials do not have the same order (which mean the coefficient vectors are not of the same length), the shorter vectors has to be modified to have the same length as the longer one by adding zeros in front. For example, to compute

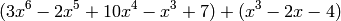
$(3x^6-2x^5+10x^4 -x^3 +7 ) + (x^3 -2x - 4)$

we first use p and q to represent the two polynomials respectively

>> p = [3  -2 10 -1 0 0 7];
>> q = [1 0 -2 -4]

The polynomial q has degree 3, we need to add 3 zeros since p has order 6:

>> p+[0 0 0 q]

ans =
     3    -2    10     0     0    -2     3

Then we read that the summation is 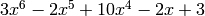$3x^6-2x^5+10x^4-2x+3$

Multiplication¶

Two polynomials can be multiplied by using the command conv which has the form:

r = conv(p,q)

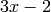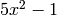where p,q are the coefficient vectors that are being multiplied and r is the coefficient vector of the product. For example, the multiplication of $3x-2$ and $5x^2-1$ is done by:

>> conv([3 -2],[5 0 -1])

ans =
    15   -10    -3     2

The result is the polynomial 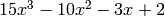$15x^3-10x^2-3x+2$ . Note that the two polynomials that are being multiplied do not have to be the same order. Multiplication of three or more polynomials is done by using conv command repeatedly.

Division¶

A polynomial can be divided by another polynomial with the command deconv that has the form:

[q,r] = deconv(u,v)

u is the numerator polynomial
v is the denominator polynomial
q is the quotient polynomial
r is the remainder polynomial

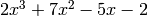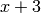For example, dividing $2x^3+7x^2-5x-2$ by $x+3$ is done by:

>> [q,r] = deconv([2 7 -5 -2],[1 3])

q =
     2     1    -8

r =
     0     0     0    22

The answer is 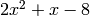$2x^2+x-8$ and the remainder is 22.

Derivatives of polynomials¶

The command polyder calculates the derivative of a single polynomial, a product of two polynomials, and a quotient of two polynomials.

k = polyder(p) returns k as the derivative of polynomial p.
k = polyder(p,q) returns k as the dervative of a product of p and q.
[n d] = polyder(p,q) returns the derivative of a quotient of two polynomials where p is the numerator and q is the denominator. The resulting derivative is in a quotient form where n is the numerator and d is the denominator.

The only difference between the last two commands is the number of the output arguments. With two output arguments MATLAB calculates the derivative of quotient of two polynomials. With one output argument, MATLAB computes the derivative of the product.

For example,

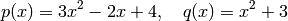
$p(x) = 3x^2-2x+4, \quad q(x) = x^2+3$

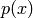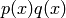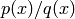The derivatives of $p(x)$ , $p(x)q(x)$ and, $p(x)/q(x)$ can be determined by:

>> p = [3 -2 4]; q = [1 0 3];
>> k = polyder(p)

k =
     6    -2

>> d = polyder(p,q)

d =
    12    -6    26    -6

>> [n d] = polyder(p,q)

n =
     2    10    -6

d =
     1     0     6     0     9

Navigation

Table Of Contents