Elementary built-in functions¶
MATLAB has a very large library of built-in functions. We can try a set of elementary functions by typing:
>> help elfun
Elementary math functions.
Trigonometric.
sin - Sine.
sind - Sine of argument in degrees.
sinh - Hyperbolic sine.
asin - Inverse sine.
asind - Inverse sine, result in degrees.
asinh - Inverse hyperbolic sine.
:
:
The help command is used to acquire some information about commands or toolboxes. Here elfun is the set of all elementary built-in functions. A function has a name and an argument in parentheses. For example, the sin function calculates the sine of a number:
>> x=pi/6, sin(x)
x =
0.5236
ans =
0.5000
We assigned a value of pi/6 to x and then calculate the value of sin(pi/3) which is 1/2. If we are still not sure how to use it, just type:
>> help sin
SIN Sine of argument in radians.
SIN(X) is the sine of the elements of X.
See also ASIN, SIND.
Overloaded methods:
codistributed/sin
The information from help gives us an instruction on how to use the sin command. Here the argument of sin is radians.
There are other categories of elementary functions such as Exponential, Complex and Rounding and remainder. Let’s see an example with complex values. MATLAB recognizes either i or j as the square root of -1:
>> i
ans =
0 + 1.0000i
>> j
ans =
0 + 1.0000i
However, both i and j can be variables too. Therefore when we assign a value to each of them, they store the new values:
>> i=5, j=8
i =
5
j =
8
For this reason, we prefer not use i and j as variables since they will return a complex value if you forget to assign values to them. Now let’s use abs and angle commands to calculate the magnitude and the phase of a complex number:
>> clear i
>> x=1+3*i, abs(x), angle(x)
x =
1.0000 + 3.0000i
ans =
3.1623
ans =
1.2490
Since we have just assigned 5 to i, we have to clear the variable i first by using the clear command. Now i will be interpreted as the square root of -1. We assign 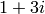 to x so its magnitude is
to x so its magnitude is 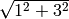 and the phase is
and the phase is 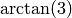 . Of course, we can check if the commands abs and ``angle` did the right thing by typing:
. Of course, we can check if the commands abs and ``angle` did the right thing by typing:
>> sqrt(1+9), atan(3)
ans =
3.1623
ans =
1.2490
Exercise¶
- A trigonometric identity is given by
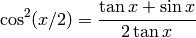
Verify that the identity is correct by calculating each side of the equation, substuting 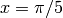
- Verify that
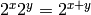 and
and 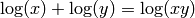 for some values of x and y. Consult the log command.
for some values of x and y. Consult the log command. - Calculate
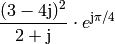
and compute its magnitude and phase.
- The roots of the equation
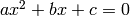 is given by
is given by 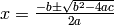 . Use this to solve
. Use this to solve 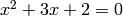 and verify the solution.
and verify the solution. - Verify the Euler’s formula
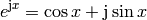
for 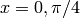 , respectively.
, respectively.
- What is an analytical form of
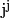 ? Is it real or complex ? Verify the Euler’s equation
? Is it real or complex ? Verify the Euler’s equation
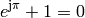
and use it to compute 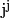 .
.