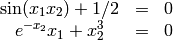Problems in Engineering¶
Solving linear equations¶
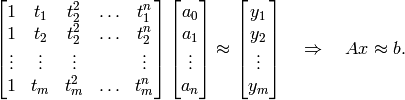
A set of 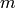 linear equations with
linear equations with 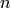 variables is given by
variables is given by
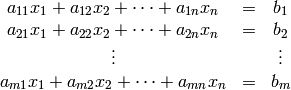
This can be written in the form of
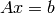
where 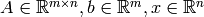 .
.
Case 1: m = n¶
When 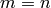 , and if
, and if 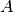 is nonsingular (
is nonsingular (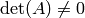 ), the solution to the linear equations is
), the solution to the linear equations is
which can be obtained by:
x = inv(A)*b
in MATLAB. However, it is recommended to use the left inverse command which is the slash \ sign. This can be done by typing:
x = A\b
This gives the same result as inv command, but the inverse of A is computed in different way (using LU decomposition). Furthermore, if A has a special structure such as symmetric, sparse, or triangular, the \ command provides an efficient algorithm to solve the linear equations. Therefore, to compute the inverse of A, it is recommended to use the following code:
A\eye(n)
where n is the size of A. When A is nonsingular, MATLAB will produce a warning message for both inv and \ commands. For such case, it depends on the vector b whether the equations has a solution or not. For example, let
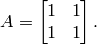
There there exists a solution if and only if 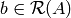 (b lies in the range space of A). For example, if
(b lies in the range space of A). For example, if ![b = [1\; 1]^T](_images/math/c75deb2815a3b5f6c60fa8d3a6543c9e86bf8832.png) , then a solution is
, then a solution is ![x = [1/2 \;1/2]^T](_images/math/bcecc9e7ab1e57cc20807ce865bade1a3f499b64.png) (and there are many more). However if
(and there are many more). However if ![b = [1 \; 0]^T](_images/math/113a4f8c5b856397101db12c556403c8eaa729b6.png) , then there is no solution x.
, then there is no solution x.
if 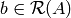 , we call the solution
, we call the solution 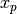 that satisfies
that satisfies 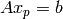 as the particular solution. Of course, there are many solutions and they can be characterized by
as the particular solution. Of course, there are many solutions and they can be characterized by 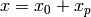 where
where 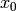 lies in the null space of A (
lies in the null space of A (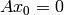 ). A set of vectors that form a basis for the null space of A can be found from the command null:
). A set of vectors that form a basis for the null space of A can be found from the command null:
>> A
A =
1 1
1 1
>> null(A)
ans =
-0.7071
0.7071
From this example, we read that any vectors lie in the null space of A is a multiple of ![[-1 \; 1]^T](_images/math/2514568fc7855700ef16a04b9c492e7fc2759e5e.png) (MATLAB just normalize the vector so that it has a unit norm). We call any vector in the null space of A as a homogeneous solution.
(MATLAB just normalize the vector so that it has a unit norm). We call any vector in the null space of A as a homogeneous solution.
Case 2: m > n (overdetermined equations)¶
The matrix A in this case is often referred to as a skinny matrix. When there are more number of equations than the number of variables, it is more likely that the solution does not exist (unless we are really lucky that b happens to be in the range space of A. An example of overdetermined equations that have a solution is
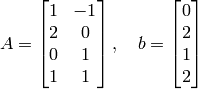
In this example, b happens to be the sum of the two columns of A (in other words, b is in the range space of A). Hence, the solution is ![x = [1 \; 1 ]^T](_images/math/45f3933f8d42d7a892894412f698bda30bbb90aa.png) .
.
However, very often in practice, when 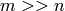 and
and 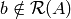 , there is no solution to Ax = b. Therefore, we resort to find a solution
, there is no solution to Ax = b. Therefore, we resort to find a solution 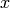 that gives
that gives 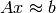 instead. By this approximation, it means Ax is closed to b in a norm-square sense. The solution x that minimizes
instead. By this approximation, it means Ax is closed to b in a norm-square sense. The solution x that minimizes
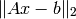
where A is a skinny matrix, is called the least-squares solution and denoted by 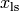 . The analytical solution can be obtained by setting the gradient of
. The analytical solution can be obtained by setting the gradient of 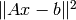 w.r.t
w.r.t 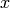 to zero. This gives
to zero. This gives
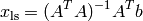
provided that 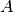 has full rank. The matrix
has full rank. The matrix 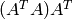 is a left inverse of
is a left inverse of 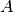 since its multiplication with
since its multiplication with 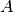 on the left hand side gives an identiy matrix. The left inverse can be computed by using pinv command. Hence, with the same example of A given above, but the vector b is
on the left hand side gives an identiy matrix. The left inverse can be computed by using pinv command. Hence, with the same example of A given above, but the vector b is ![b = [1 \; 0 \; 0 \; 0 ]^T](_images/math/54c4bd11118fd75f95789deef666d89434b40713.png) . Then there is NO solution to Ax = b, but the least-square solution is:
. Then there is NO solution to Ax = b, but the least-square solution is:
>> pinv(A)*b
ans =
0.1667
-0.3333
Another way to use \ command. It also computes the least-square solution when m > n:
>> A\b
ans =
0.1667
-0.3333
Case 3: m < n (underdetermined equations)¶
In this case, A is a fat matrix. When there are more number of variables than the number of equations, if a solution exists, the solution will not be unique. This can be explained by the following argument. Since A is fat, rank of A is less than or equal to m, and that certainly implies the null space of A is nonzero. Then there will be a nonzero 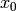 such that
such that 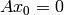 . This means if
. This means if 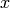 is any solution to
is any solution to 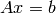 then so is
then so is 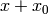 . A homogeneous solution
. A homogeneous solution 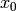 can be found using the null command. For example,
can be found using the null command. For example,
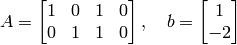
A solution is ![x_p = [a \; a-3 \; 1-a \;b ]^T](_images/math/514258ff6102a68cea36cf7d0ea4ad122fca33fc.png) where
where 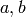 can be any number. Using the null command to find a solution to
can be any number. Using the null command to find a solution to 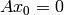 gives:
gives:
>> null(A)
ans =
-0.5774 0
-0.5774 0
0.5774 0
0 1.0000
Then we read that any linear combination of the above two vectors is a homogeneous solution 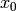 . So the solutions to Ax=b are not unique and there are infinite number of solutions.
. So the solutions to Ax=b are not unique and there are infinite number of solutions.
This lead us to consider a solution that has a special property or satisfies some extra conditions. The \ command in MATLAB gives a solution to Ax=b that most entries of x are zero. With the same example of A,b given above, we know that a solution can be written as ![x_p = [a \; a-3 \; 1-a \;b ]^T](_images/math/514258ff6102a68cea36cf7d0ea4ad122fca33fc.png) (where a,b are free numbers). When we use \ command it gives:
(where a,b are free numbers). When we use \ command it gives:
>> x = A\b
ans =
0
-3.0000
1.0000
0
(MATLAB sets the free variables to zero.)
For most cases in practice, we are interested in a solution x that has the smallest size. This means we find 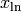 such that
such that

where  is the optimization variable. In other words, we explore a set of solutions to Ax=b and pick the one that has the mininum norm. Such solution is referred as the least-norm solution and denoted by
is the optimization variable. In other words, we explore a set of solutions to Ax=b and pick the one that has the mininum norm. Such solution is referred as the least-norm solution and denoted by  . The analytical form of the least-norm solution is given by
. The analytical form of the least-norm solution is given by
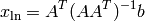
provided that 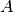 has full rank. The matrix
has full rank. The matrix 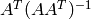 is a right inverse of
is a right inverse of 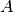 since its multiplication with
since its multiplication with 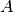 on the right hand side gives an identity matrix. The right inverse is obtained in MATLAB from the pinv command (pseudo inverse). Therefore, the least-norm solution can be computed by:
on the right hand side gives an identity matrix. The right inverse is obtained in MATLAB from the pinv command (pseudo inverse). Therefore, the least-norm solution can be computed by:
>> x1 = pinv(A)*b
x1 =
1.3333
-1.6667
-0.3333
0
We can verify that both the solutions x (from \ command) and x1 (the least-norm solution) solve Ax=b exactly:
>> A*x-b
ans =
1.0e-15 *
0.2220
0
>> A*x1-b
ans =
1.0e-15 *
-0.3331
0.4441
However, in principle x1 must have a smaller norm than x. So, we can check it easily by computing their norms:
>> norm(x)
ans =
3.1623
>> norm(x1)
ans =
2.1602
and the result is affirmative.
Another related command in linear albegra is the rank command. It is used to compute the rank of a matrix, which is, by definition, the number of independent column vector of that matrix. For example:
>> A = [1 1 1;2 2 2]
A =
1 1 1
2 2 2
>> rank(A)
ans =
1
Linear least-squares¶
A linear least-squares problem is motivated from solving linear overdetermined equations
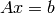
where 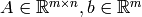 and
and 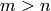 . In a lot of cases, we cannot solve the equations exactly, so we find a solution
. In a lot of cases, we cannot solve the equations exactly, so we find a solution 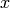 that gives the best approximation of Ax to b instead. Mathematically, we solve
that gives the best approximation of Ax to b instead. Mathematically, we solve
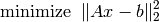
where 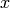 is the opitmization variable. To find the analytical solution, we expand the cost objective by
is the opitmization variable. To find the analytical solution, we expand the cost objective by
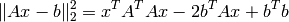
Setting the gradient to zero gives
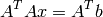
Therefore, if 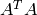 is nonsingular (which is equivalent to A is full rank), then the least-squares solution is given by
is nonsingular (which is equivalent to A is full rank), then the least-squares solution is given by
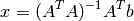
We do not actually compute the least-squares solution from this expression, but rather use the command A\b. If m=n, the command A\b simply means 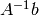 , and when m > n, the command A\b produces the least-squares solution.
, and when m > n, the command A\b produces the least-squares solution.
Curve fitting¶
A typical example of least-squares application is a polynomial fitting problem. Suppose we have data points 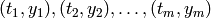
Suppose we generate these data sets according to:
>> m = 100; t = linspace(0,10,m)';
>> y = 0.1*t.^3-t.^2+3*randn(m,1);
>> plot(t,y,'x','linewidth',2);
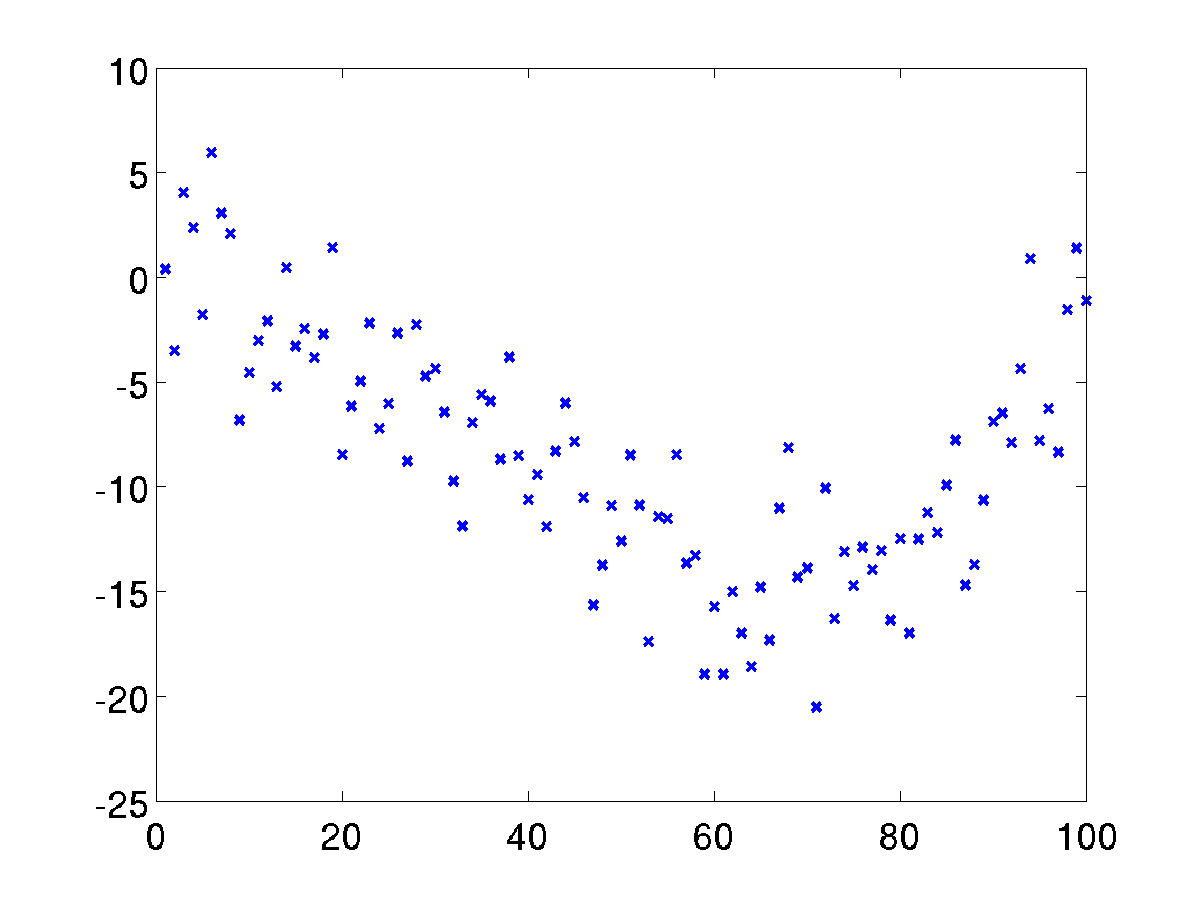
The goal is to fit a polynomial of order 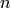 ,
, 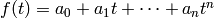 to these data at the given points
to these data at the given points 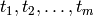 . This is the problem of finding
. This is the problem of finding 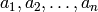 such that
such that
Fiting a polynomial of order 1 (an affine function) using the least-squares approach can be done easily by constructing the corresponding matrices A,b by:
b = y;
for n=1:3,
A = zeros(m,n)
for k=0:n,
A(:,k+1) = t.^k;
end;
x = A\b;
plot(t,A*x,'linewidth',2);
end
legend('data','order 1','order 2','order 3');
(with a change in line style manually.) The result can be shown in the following figure.
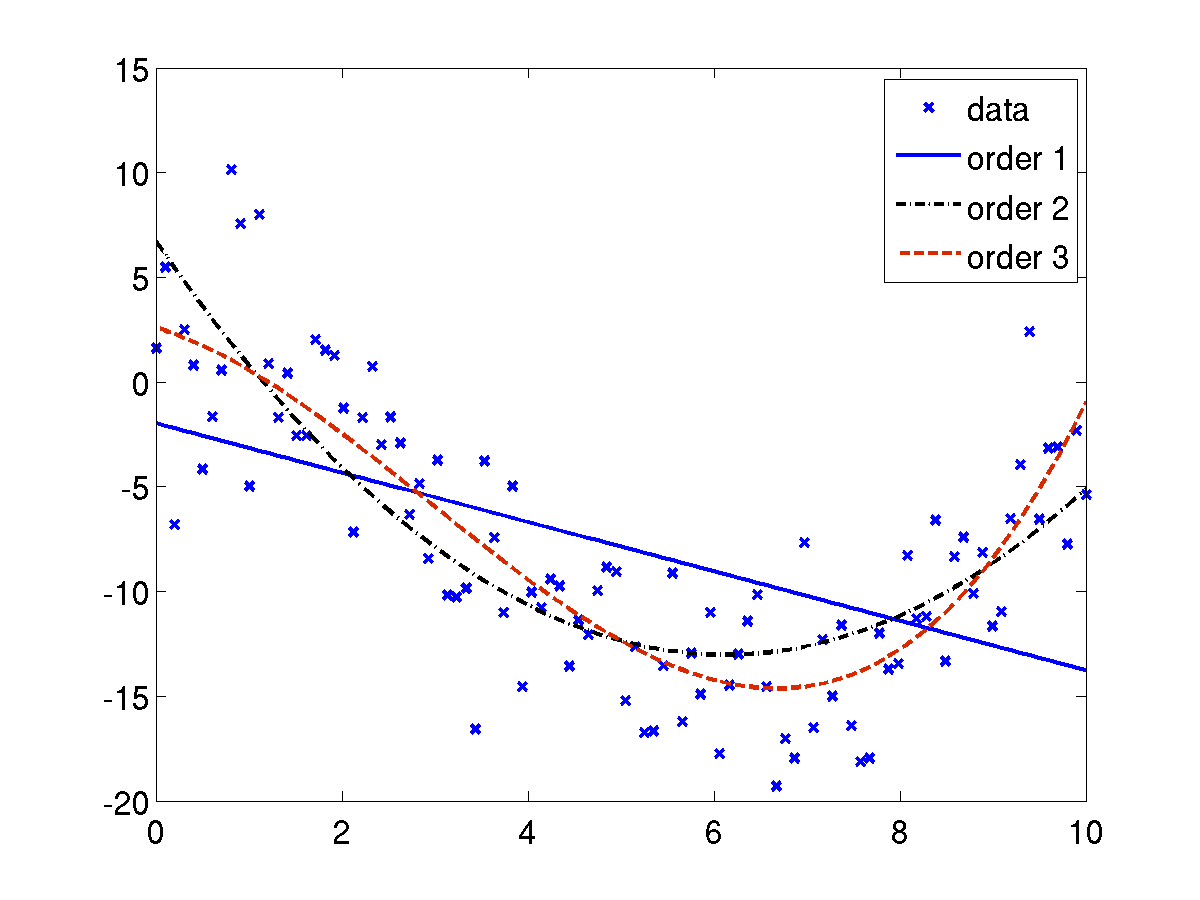
The coefficients of the polynomial for n=3 is kept in the variable x and their values are:
>> x =
2.5946
-1.3766
-0.7479
0.0850
Therefore, the polynomial of order 3 that fits best to the given data points is
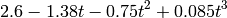
Curve fitting problems can be solved with a MATLAB built-in function called polyfit. This command also uses the least-squares method. The basic form of the function is:
p = polyfit(x,y,n)
where
- x is a vector with the horizontal coordinate of the data points
- y is a vector with the vertical coordinate of the data points
- n is the degree of the polynomial
- p the vector of the coefficients of the polynomial that fits the data
Let’s try with the same example. Using polyfit to fit a 3rd-order polynomial with the data gives:
>> p = polyfit(t,y,3)
p =
0.0850 -0.7479 -1.3766 2.5946
This gives the same answer as we had earlier. Notice that the first element of p correspond to the highest power of the polynomial.
In many situations, it is required to fit functions other than polynomials. For example,
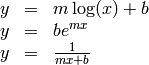
In order to apply a least-squares method, we have to write the relation between x and y such that it is linear mapping in the function parameters. For example, the last two functions can be rewritten as
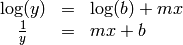
This means that the polyfit can be used to determine the best fit for the parameters 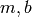 .
.
For 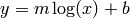 , use:
, use:
p = polyfit(log(x),y,1)
For 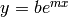 or
or 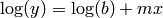 use:
use:
p = polyfit(x,log(y),1)
For 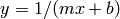 or
or 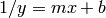 , use:
, use:
p = polyfit(x,1./y,1)
The result is assigned to p which is a row vector of two elements. The first element p(1) corresponds to m and the second element p(2) corresponds to b.
Exercises¶
- The relationship between two variables
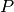 and
and 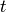 is known to be:
is known to be:
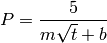
where 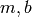 are parameters to be determined. The following data points are known:
t = 1,2,3,4,5,6,7 and P = 8.9,3.4,2.1,2.0,1.6,1.3,1.2. Determine
are parameters to be determined. The following data points are known:
t = 1,2,3,4,5,6,7 and P = 8.9,3.4,2.1,2.0,1.6,1.3,1.2. Determine 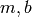 by solving a curve fitting problem.
by solving a curve fitting problem.
- A variable
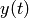 satisfies
satisfies
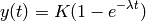
where 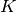 is a given constant, and
is a given constant, and 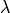 is the parameter to determined. Given the values of
is the parameter to determined. Given the values of 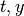 from this data and
from this data and 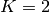 , use the least-squares approach to find
, use the least-squares approach to find 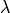 .
.
- Fit the curve
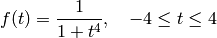
with a polynomial function of degree 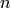 . Vary the values of
. Vary the values of 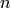 and compare the results.
and compare the results.
- The viscosity of gases are typically modeled by
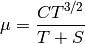
where 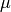 is the viscosity (Ns/m^3),
is the viscosity (Ns/m^3), 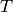 is the absolute temperature (C), and
is the absolute temperature (C), and 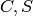 are empirical constants. Using the data below to determine the constants
are empirical constants. Using the data below to determine the constants 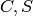 :
:
>> T = [-20 0 40 100 200 300 400 500 1000];
>> mu = [1.63 1.71 1.87 2.17 2.53 2.98 3.32 3.64 5.04];
Probability and Statistics¶
A probability density function (pdf) of a random variable can be computed by pdf command which has the form:
>> f = pdf(name,x,A,B,C);
- name is the distribution name such as norm (Normal), exp (Exponential), etc.
- x is a vector contains all the points at which the pdf is calculated.
- A,B,C are parameters associated with the distribution.
For example, evaluating the Gaussian distribution function with mean 1 and variance 2 can be done by:
>> x=linspace(-3,3,100);
>> f=pdf('norm',x,1,2);
>> plot(x,f);
The cumulative distribution function (which is the area under the distribution curve)
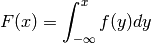
is computed by cdf command which has the form:
>> F = cdf(name,x,A,B,C);
where the input arguments have the same description as the pdf command. The cumulative function must start from 0 and converge to 1 as the value of x increases. For example, we show the cumulative distribution function of a binomial variable with parameters n=10, p = 0.5. This can be done by typing:
>> n = 10; p = 1/2;
>> x = 0:n;
>> F=cdf('binomial',x,n,p);
>> stairs(x,F);
(For discrete random variables, the pdf and cdf are typically plots using stairs command.)
Suppose we have sample values from a given distribution. The histogram of these data should resemble the density function in the long run. For example, we generate 1000 points of Gaussian variables z and a vector x with values starting from -3 to 3. We calculate the histogram of z using the hist command and compare the graphs as described below:
>> x = linspace(-3,3,100);
>> z = randn(1,1000);
>> f = hist(z,x);
>> bar(x,f); hold on;
>> plot(x,pdf('norm',x,0,1);
Optimization¶
A common problem in optimization is to find the solution to
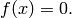
The solution 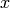 is the value of
is the value of 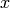 where the function cross the x axis. A numerical solution can be obtained by applying an iterative algorithm where the iteration stops when the difference in
where the function cross the x axis. A numerical solution can be obtained by applying an iterative algorithm where the iteration stops when the difference in 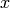 between two iterations is smaller than some measure. The function
between two iterations is smaller than some measure. The function 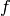 can be a function of several variables (which means
can be a function of several variables (which means 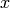 is a vector.) In general a function can have none, one, several, or infinite number of solutions.
is a vector.) In general a function can have none, one, several, or infinite number of solutions.
MATLAB provides a built-in function called fzero to compute the roots of a scalar-valued function. It has the form:
x = fzero(function,x0)
x is the solution, which is a scalar
- function is the function to be solved. It can be expressed in different ways:
- The function is entered as a string.
- The function is defined as a user-defined function.
- The function is created as an anonymous function.
x0 can be a scalar or a two-element vector. If it is a scalar, it is a value of x near the point where the function crosses the x axis. If x0 is a vector of length two, fzero assumes x0 is an interval where the sign of f(x0(1)) differs from the sign of f(x0(2)). An error occurs if this is not true.
To find a good starting point x0, we can make a plot of the function to check where it crosses the x axis approximately.
For example, let us determine the solution of the equation
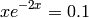
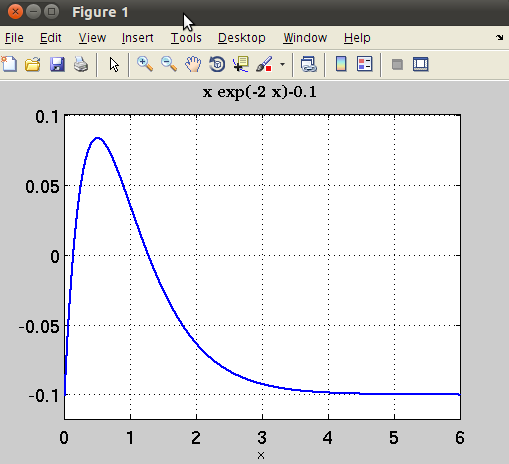
First we plot the function 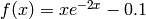 :
:
>> ezplot('x*exp(-2*x)-0.1',[0 6]);grid;
The plot shows that the function has two solutions; one is close to zero, and the other one is between 1 and 2. The first solution can be found by using:
>> x1 = fzero('x*exp(-2*x)-0.1',0.1)
x1 =
0.1296
We can enter the function description as an anonymous function and find the second root as shown below:
>> F=@(x)x*exp(-2*x)-0.1
F =
@(x)x*exp(-2*x)-0.1
>> fzero(F,2)
ans =
1.2713
When the function 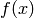 is a function of several variables, the roots of the function can be found by using the fsolve command which has the form:
is a function of several variables, the roots of the function can be found by using the fsolve command which has the form:
x = fsolve(fun,x0)
where fun is a function that accepts a vector and returns a vector, x0 is an initial point, and x is the solution.
For example, we want to solve the system of two equations and two unknowns:
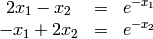
We can write these equations in the form of 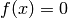 as
as
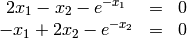
First write the function description as a user-defined function:
function[F] = myfun(x)
F = [2*x(1) - x(2) - exp(-x(1));
-x(1) + 2*x(2) - exp(-x(2))];
You must save this function file as myfun.m on your current directory. Next, define a starting point and call fsolve. Make sure that the function 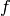 is refered by using @ sign:
is refered by using @ sign:
>> x0 = [-5; -5];
>> x = fsolve(@myfun,x0);
Equation solved.
fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.
<stopping criteria details>
x =
0.5671 0.5671
Therefore the commands fsolve and fzero can be used to find a solution of an unconstrained optimization problem:
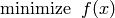
since the optimality condition, which is the zero gradient condition:
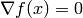
is equivalent to finding the roots of some function.
For example, we wish to find the maximum value of the function 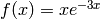 for
for 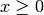 . The plot of this function:
. The plot of this function:
>> ezplot('x*exp(-3*x)',[0 10])
shows that the maximum occurs at a value between 0 and 1. The gradient of this function is 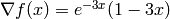 . Therefore, the maximum can be found by:
. Therefore, the maximum can be found by:
>> x = fsolve('exp(-3*x)*(1-3*x)',0.5)
Equation solved.
fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.
<stopping criteria details>
x =
0.3333
MATLAB also provides fminbnd command for finding a local minimum or maximum within a given interval. The command has the form:
[x,fval] = fminbnd(fun,x1,x2)
- x is the value where the function has a minimum
- fun is the function defined as a string, an anonymous function, or a user-defined function.
- x1,x2 is the interval of x.
Within a given interval, the minimum of a function can either be at the boundary of the interval, or at a point within the interval. The fminbnd looks for a local minimum and if it is found, the minimum will be compared with the function values at the boundary of the interval. Then MATLAB will returns the point with the actual minimum value of the interval.
For example, consider the function
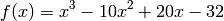
on the interval 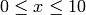 , as shown in the figure.
, as shown in the figure.
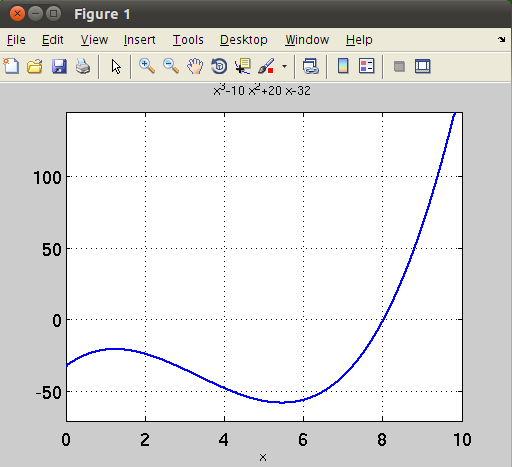
From the figure, a local minimum occurs between 4 and 6. Its location can be found by:
>> F=@(x) x^3-10*x^2+20*x-32;
>> [x,fval]=fminbnd(F,4,6)
x =
5.4415
fval =
-58.1468
If we change the interval to [8,10], obviously the minimum must occur at the boundary, which is x=8. Let’s verify by typing:
>> [x,fval]=fminbnd(F,8,10)
x =
8.0000
fval =
0.0025
To find a local maximum of this function which occurs at a point between 0 and 2, we must redefine the function F as -F (since maximizing F is equivalent to minimizing -F.):
>> G=@(x) -(x^3-10*x^2+20*x-32);
>> [x,fval] = fminbnd(G,0,2)
x =
1.2251
fval =
20.6680
Exercises¶
- The Van der Waals equation gives the relationship between these quantities for a real gas by:
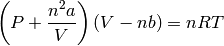
where 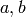 are constants that are specific for each gas. Use the fzero function to calculate the volume of 2 mol
are constants that are specific for each gas. Use the fzero function to calculate the volume of 2 mol 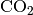 at temperature of 50C and pressure of 6 atm. For
at temperature of 50C and pressure of 6 atm. For 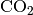 ,
, 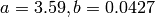 .
. 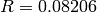 is the gas constant. An initial point can be chosen from the ideal gas equation:
is the gas constant. An initial point can be chosen from the ideal gas equation:
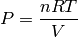
- Determine the solution of the equation
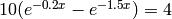 .
. - Determine the three positive roots of the equation
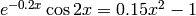 .
. - Determine the positive roots of the equation
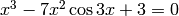 .
. - Determine the minimum of the function
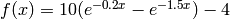 .
. - Solve the nonlinear equations: